Gửi đến bạn đọc tổng hợp các khái niệm cơ bản và bài tập về lý thuyết đồ thị toán rời rạc cùng lời giải chi tiết, giúp bạn hiểu sâu hơn và vận dụng tốt hơn vào học tập.
Xem thêm:
đường đi và chu trình euler
I. Lý thuyết đồ thị toán rời rạc
1. Đường đi
Đường đi độ dài n từ đỉnh u đến đỉnh v trên đồ thị vô hướng \(G=<V,E>\) là dãy:
\(x_{0}, x_{1},…, x_{n-1}, x_{n}\)
Trong đó:
- n là số nguyên dương
- \(x_{0} = u, x_{n} = v\)
- \((x_{i}, x_{i+1}) ∈E, i =0, 1, 2,…, n-1\)
Đường đi như trên còn có thể biểu diễn thành dãy các cạnh:
\((x_{0},x_{1}), (x_{1},x_{2}),…, (x_{n-1},x_{n}) \\\)Ví dụ 1: Tìm các đường đi, chu trình trong đồ thị vô hướng:
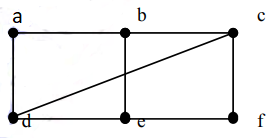
Lời giải
a, d, c, f, e là đường đi đơn độ dài 4. d, e, c, a không là đường đi vì (e,c) không phải là cạnh của đồ thị. Dãy b, c, f, e, b là chu trình độ dài 4. Đường đi a, b, e, d, a, b có độ dài 5 không phải là đường đi đơn vì cạnh (a,b) có mặt hai lần.
Ví dụ 2: Trên đồ thị vô hướng cho trong hình:
– a, d, c, f, e là đường đi đơn độ dài 4.
– d, e, c, a không là đường đi, do (c,e) không phải là cạnh của đồ thị.
– Dãy b, c, f, e, b là chu trình độ dài 4.
– Đường đi a, b, e, d, a, b có độ dài là 5 không phải là đường đi đơn, do cạnh (a, b) có mặt trong nó 2 lần.
2. Chu trình
Đỉnh u được gọi là đỉnh đầu, đỉnh v được gọi là đỉnh cuối của đường đi. Đường đi có đỉnh đầu trùng với đỉnh cuối (u=v) được gọi là một chu trình. Đường đi hay chu trình được gọi là đơn nếu như không có hai cạnh nào lặp lại.
3. Đồ thị liên thông
Đồ thị vô hướng được gọi là liên thông nếu luôn tìm được đường đi giữa hai đỉnh bất kỳ của nó.
Trong trường hợp đồ thị G=<V, E> không liên thông, ta có thể phân rã G thành một số đồ thị con liên thông mà chúng đôi một không có đỉnh chung. Mỗi đồ thị con như vậy được gọi là một thành phần liên thông của G.
Ví dụ: Tìm các thành phần liên thông của đồ thị

Số thành phần liên thông của G là 3. Thành phần liên thông thứ nhất gồm các đỉnh 1, 2, 3, 4, 6, 7. Thành phần liên thông thứ hai gồm các đỉnh 5, 8, 9, 10. Thành phần liên thông thứ ba gồm các đỉnh 11, 12, 13.
II. Bài tập lý thuyết đồ thị toán rời rạc có lời giải
Bài 1: Tính số đỉnh của đồ thị
a. Một đồ thị có 15 cạnh với 3 đỉnh bậc 4, các đỉnh còn lại đều bậc 3, hỏi đồ thị
có bao nhiêu đỉnh?
Lời giải
Gọi A là số đỉnh bậc 3 của đồ thị, ta có tổng số bậc của đồ thị là: 3*4+A*3 =
12+3A.
Ta có tổng số bậc của đồ thị bằng hai lần số cạnh:
12+3A = 2.15 = 30
3A = 18 => A = 6.
Vậy đồ thị có 3 + 6 = 9 đỉnh.
Bài 2: Một đơn đồ thị liên thông có 10 mặt, tất cả các đỉnh đều có bậc bằng 4, tìm số đỉnh của đồ thị.
Lời giải
Gọi f là số miền của mặt phẳng bị chia bởi biểu diễn phẳng của đồ thị, e là số cạnh và v là số đỉnh của đồ thị
Ta có tổng bậc của đồ thị bằng 2 lần số cạnh, tức là : 2e = 4v => e=2v
Mặt khác, ta có : f = e – v + 2 => 10 = 2v – v + 2 => v=8
Vậy đồ thị có 8 đỉnh và 16 cạnh.
Bài 3: Một đơn đồ thị liên thông có 10 mặt, tất cả các đỉnh đều có bậc bằng 4, tìm số đỉnh của đồ thị.
Lời giải
Gọi f là số miền của mặt phẳng bị chia bởi biểu diễn phẳng của đồ thị, e là số cạnh và v là số đỉnh của đồ thị
Ta có tổng bậc của đồ thị bằng 2 lần số cạnh, tức là : 2e = 4v => e=2v
Mặt khác, ta có : f = e – v + 2 => 10 = 2v – v + 2 => v=8
Vậy đồ thị có 8 đỉnh và 16 cạnh.
Trên đây là các khái niệm cơ bản và một số bài tập về lý thuyết đồ thị toán rời rạc. Cảm ơn bạn đã tham khảo trên ttnguyen.net
Bài viết cùng chủ đề: