Trong lý thuyết xác suất thống kê, phân phối chuẩn còn được gọi là phân phối Gauss. Phân phối này còn được biết đến với tên gọi “đường cong hình chuông” (bell curve) vì đồ thị của nó có dạng đối xứng và đỉnh tròn như một chiếc chuông. Trong bài viết này, TTnguyen sẽ chia sẻ định nghĩa, công thức và bài tập phân phối chuẩn kèm lời giải chi tiết.
Xem thêm:
bài tập kiểm định giả thuyết thống kê
1. Phân phối chuẩn là gì?
1.1. Định nghĩa
Phân phối chuẩn (phân phối Gauss) là một phân phối xác suất liên tục đối xứng xung quanh giá trị trung bình của nó, hầu hết các quan sát tập hợp xung quanh đỉnh trung tâm và xác suất đối với các giá trị xa trung bình giảm dần theo cả hai hướng. Các giá trị cực trị ở cả hai phía của phân phối là khó xảy ra tương tự.
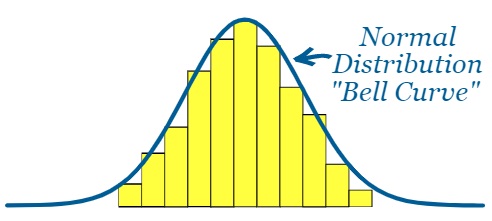
Đường cong màu xanh lam là phân phối chuẩn. Màu vàng biểu đồ hiển thị một số dữ liệu
theo sau nó một cách chặt chẽ, nhưng không hoàn hảo (điều này là bình thường).
Ở dạng đồ họa, phân phối chuẩn xuất hiện dưới dạng đường cong hình chuông “Bell Curve” vì nó trông giống như một cái chuông.

Phân phối chuẩn thường được sử dụng để mô tả:
- Chiều cao của một người
- Kích thước của những thứ do máy móc sản xuất
- Sai số trong phép đo
- Huyết áp
- Điểm trong bài kiếm tra
- Điểm IQ
Trong xác suất thống kê, phân phối chuẩn tắc là một trường hợp đặc biệt của phân phối chuẩn với trung bình μ = 0 và độ lệch chuẩn σ = 1.
Xem thêm:
phân phối nhị thức: Công thức, định nghĩa và bài tập có lời giải
Bài tập công thức bernoulli xác suất có lời giải
Tổng hợp công thức thống kê – Từ a -z có ví dụ mẫu
1.2. Đặc điểm của phân phối chuẩn là gì?
Đặc điểm chính:
- Đối xứng: Đường cong phân phối chuẩn đối xứng qua giá trị trung bình.
- Tập trung cao: Phần lớn các giá trị tập trung gần giá trị trung bình, trong khi xác suất của các giá trị cực đoan giảm dần ở hai phía.
- Độ lệch chuẩn: Xác định độ rộng và hình dạng của đường cong. Độ lệch chuẩn càng nhỏ, đường cong càng hẹp; ngược lại, độ lệch chuẩn càng lớn, đường cong càng phẳng
2. Công thức phân phối chuẩn
Để được coi là phân phối chuẩn, một tập dữ liệu (khi được vẽ đồ thị) phải tuân theo một đường cong đối xứng hình chuông có tâm xung quanh giá trị trung bình. Công thức phân phối chuẩn trong thống kê được đưa ra bởi:
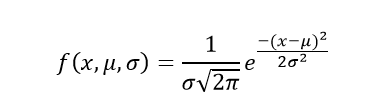
Trong đó:
- x: giá trị của biến hoặc dữ liệu đang được kiểm tra và f (x) hàm xác suất
- μ: trung bình
- σ: độ lệch chuẩn
Nếu độ lệch chuẩn (σ) càng nhỏ, dữ liệu càng gần nhau và biểu đồ trở nên hẹp hơn. Nếu độ lệch chuẩn càng lớn, dữ liệu sẽ bị phân tán nhiều hơn và biểu đồ trở nên rộng hơn. Độ lệch chuẩn được sử dụng để chia nhỏ diện tích dưới đường cong thông thường. Mỗi phần được chia nhỏ xác định tỷ lệ phần trăm dữ liệu nằm trong vùng cụ thể của biểu đồ.
3. Đồ thị và bảng phân phối
Đồ thị phân phối chuẩn có dạng hình chuông đối xứng. Các khu vực dưới đường cong được chia thành các tỷ lệ phần trăm nhất định:
- 68% dữ liệu nằm trong khoảng ±1 độ lệch chuẩn.
- 95% dữ liệu nằm trong khoảng ±2 độ lệch chuẩn.
- 99,7% dữ liệu nằm trong khoảng ±3 độ lệch chuẩn.
4. Các tính phân phối chuẩn
Để tính xác suất hoặc giá trị liên quan đến phân phối chuẩn:
- Sử dụng công thức hàm mật độ xác suất.
- Sử dụng bảng phân phối chuẩn tắc (bảng Z).
- Áp dụng công cụ thống kê hoặc phần mềm hỗ trợ.
5. Bài tập phân phối chuẩn có lời giải
Câu 1: Tính hàm mật độ xác suất của phân phối chuẩn sử dụng dữ liệu sau. x = 3, μ = 4 và σ = 2.
Lời giải:
Cho trước, biến số, x = 3, trung bình = 4 và độ lệch chuẩn = 2
Bằng công thức mật độ xác suất của phân phối chuẩn, chúng ta có thể viết:
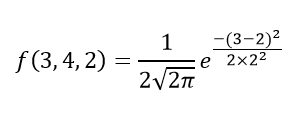
Vậy, f(3,4,2) = 1.106.
Câu 2: Nếu giá trị của biến ngẫu nhiên là 2, giá trị trung bình là 5 và độ lệch chuẩn là 4 thì hãy tìm hàm mật độ xác suất của phân phối gaussian.
Giải
Ta có Biến, x = 2,trung bình = 5 và độ lệch chuẩn = 4
Bằng công thức mật độ xác suất của phân phối chuẩn, chúng ta có thể viết;
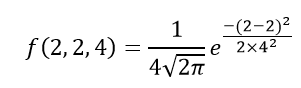
f (2,2,4) = 1 / (4√2π) là 0
f (2,2,4) = 0,0997
Câu 3: Tìm xác suất để biến ngẫu nhiên phân phối chuẩn hóa nhận giá trị:
a) Trong khoảng (-2,33; 2,33)
b) Trong khoảng (-2; 1)
c) Trong khoảng (-0,89; 2,5)
d) Lớn hơn 3,02
e) Nhỏ hơn 2,5
Giải

Câu 4: Biến ngẫu nhiên X tuân theo quy luật chuẩn với μ =10,δ= 2. Tính xác suất để X
nhận được giá trị trong khoảng ( 8;12)
Giải

Câu 5: Trong hệ thống tỷ giá hối đoái thả nổi, sự biến đổi của tỷ giá hối đoái thả nổi, sự
biến động của tỷ giá hối đoái chịu sự tác động của rất nhiều nhân tố và có thể xem như biến
ngẫu nhiên phấn phối chuẩn, giả sử ở một giai đoạn nào đó tỷ giá của USD với VND có
trung bình là 15000đ và độ lệch chuẩn là 500đ. Tìm xác suất để trong một ngày nào đó.
a) Tỷ giá sẽ cao hơn 16000đ
b) Tỷ giá sẽ thấp hơn 14500đ
c) Nằm trong khoảng 14500đ đến 16500
Giải
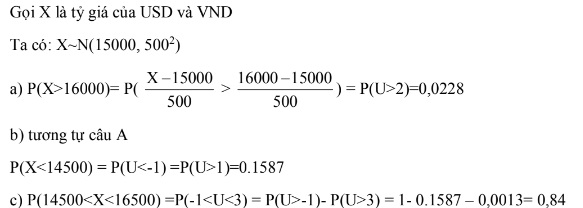
Câu 6: Việc tiêu dùng điện hàng tháng của các hộ gia đình ở Hà Nội là biến ngẫu nhiên
phân bố chuẩn với trung bình là 200KWh và độ lệch chuẩn là 40KWh. Tìm xác suất để chọn
ngẫu nhiên một hộ gia đình thì hộ đó:
a. Có mức tiêu dùng điện hàng tháng trên 250KWh
b. Có mức tiêu dùng điện hàng tháng dưới 180KWh
Giải

Câu 7: Chiều cao nam giới khi trưởng thành ở một vùng dân cư là biến ngẫu nhiên phân
phối chuẩn với μ=160 cm và σ=6cm . Một thanh niên bị coi là lùn nếu có chiều cao nhỏ hơn
155cm
a) Tìm tỷ lệ thanh niên lùn ở vùng đó
b) Tìm xác suất để lấy ngẫu nhiên 4 người thì có ít nhất 1 người không bị lùn.
Giải

Câu 8: Kích thước chi tiết là biến ngẫu nhiên phân phối chuẩn với 50. Kích thước thực
tế của các chi tiết không nhỏ hơn 32cm và không lớn hơn 68cm. Tìm xác suất để lấy ngẫu
nhiên một chi tiết có kích thước.
a) Lớn hơn 55cm
b) Nhỏ hơn 40cm
Giải

Các câu hỏi thường gặp
Ý nghĩa của phân phối chuẩn
Phân phối chuẩn mô tả một đồ thị dữ liệu đối xứng xung quanh giá trị trung bình của nó, trong đó độ rộng của đường cong được xác định bởi độ lệch chuẩn. Nó được mô tả trực quan là “đường cong hình chuông”.
Tại sao lại gọi là phân phối chuẩn
Về mặt kỹ thuật, phân phối chuẩn được gọi là phân bố Gauss, tuy nhiên nó sử dụng thuật ngữ “bình thường” sau các ấn phẩm khoa học vào thế kỷ 19 cho thấy nhiều hiện tượng tự nhiên dường như “lệch bình thường” so với giá trị trung bình. Ý tưởng về “độ biến thiên bình thường” này đã được nhà tự nhiên học Sir Francis Galton phổ biến như một “đường cong bình thường” trong tác phẩm năm 1889 của ông, Natural Inheritance.
Phân phối chuẩn được sử dụng để làm gì?
Phân phối chuẩn có ý nghĩa quan trọng trong thống kê và thường được sử dụng trong khoa học tự nhiên và nghệ thuật xã hội để mô tả các biến ngẫu nhiên có giá trị thực mà phân phối của chúng không xác định
Làm thế nào để bạn biết nếu dữ liệu được phân phối bình thường?
Biểu đồ trình bày một biểu diễn đồ họa hữu ích của dữ liệu đã cho. Khi biểu đồ phân phối được chồng lên với đường cong chuẩn của nó, thì phân phối được gọi là phân phối chuẩn.
Làm thế nào để bạn sử dụng một bảng phân phối chuẩn?
Như chúng ta đã biết, nhãn cho các hàng chứa phần nguyên và chữ số thập phân đầu tiên của z. Ngược lại, tiêu đề cho các cột bao gồm chữ số thập phân thứ hai của z. Các giá trị trong bảng là xác suất tương ứng với loại bảng. Do đó, để nhận giá trị 0,56 từ bảng z, hãy xác định giá trị xác suất tương ứng với hàng 0,5 và cột 0,06 (= 0,2123).
Trên đây là bài viết về định nghĩa, công thức và một số vài bài tập vận dụng phân phối chuẩn. Nếu có gì sai sót hoặc thắc mắc thì đừng ngần ngại liên hệ với mình nhé! Cảm ơn bạn đã tham khảo trên ttnguyen.net
Bài viết cùng chủ đề: