Bài toán tìm m để hệ phương trình có nghiệm tầm thường và nghiệm không tầm thường là dạng toán thường gặp trong đại số tuyến tính. Sau đây, chúng ta sẽ tìm hiểu điều kiện và một số bài tập nhé!
Xem thêm:
Nghiệm không tầm thường là gì?
Nghiệm không tầm thường (vô số nghiệm) của một hệ phương trình tuyến tính thuần nhất n ẩn số là hạng của ma trận hệ số nhỏ hơn số ẩn: rank(A)<n.
Nghiệm tầm thường là gì?
Một hệ phương trình thuần nhất có một nghiệm tầm thường (nghiệm duy nhất) khi và chỉ khi hạng của ma trận bằng số ẩn.
Điều kiện để hệ có nghiệm tầm thường (vô số nghiệm)
Cho hệ phương Ax=0 là hệ có n ẩn, điều kiện để hệ có nghiệm tầm thường, không tầm thường là:
- Hệ có nghiệm duy nhất (nghiệm tầm thường): rank(A)=n
- Hệ có vô số nghiệm (nghiệm không tầm thường): rank(A)<n
- Đối với ma trận vuông: detA= 0 => vô số nghiệm
Bài viết liên quan:
Bài tập nghiệm không tầm thường
Tìm m để hệ phương trình có nghiệm duy nhất toán cao cấp
Cho ma trận sau: Tìm m để hệ có nghiệm duy nhất
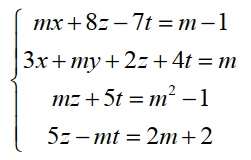
Giải
Để hệ phương trình có nghiệm duy nhất thì detA ≠0=> m≠0
Tìm m để hệ có nghiệm không tầm thường
Hướng dẫn giải
Xem thêm: giải và biện luận hệ phương trình tuyến tính theo tham số m
Tìm m để hệ có nghiệm tầm thường
Tìm m để hệ phương trình vô số nghiệm toán cao cấp
Hướng dẫn giải
Trên đây là một số bài tập tìm m để hệ phương trình có nghiệm tầm thường và không tầm thường. Cảm ơn các bạn đã tham khảo trên ttnguyen.net
Tải tài liệu nghiệm không tầm thường PDF:
Có thể bạn quan tâm:
